At SHOT, I was discussing something with an ammo manufacturer and the question of muzzle energy came up. Not “does muzzle energy matter?” but simply how to calculate it. I was very surprised to learn that this manufacturer was unfamiliar with the 2.22 Rule.
The standard equation is:
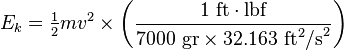
Where m is the mass of the bullet (in grains) and v is the velocity (in feet per second). Easy, right? Let’s use an example of a 147gr bullet at 950fps:
73.5 * 950 * 950 ÷ 7000 ÷ 32.163 = 294.7 ft-lbs ME
But the 2.22 Rule gives a quick and dirty way to calculate muzzle energy:
- bullet weight (divided by 100)
- times muzzle velocity (divided by 100)
- times muzzle velocity (divided by 100)
- times 2.22
For a 147gr bullet traveling at 950fps:
1.47 * 9.5 * 9.5 * 2.22 = 294.5 ft-lbs ME
Close enough for me. The major benefits of the 2.22 Rule are that it is easy to remember (as opposed to memorizing the acceleration due to gravity of 32.163 used for ammunition) and it can be done on any simple calculator.
Train hard & stay safe! ToddG
(Muzzle energy equation graphic courtesy Wikipedia.com)
Muzzle energy is import so that the bullet can do its work (which is making deep and wide hole), but we aren’t talking laser ray guns. The mythical “energy dump” is just that.
Ding ding ding! Dandapani moves to the front of the class.
Everything would be easier if they just used SI units, like everyone else who does important calculations.
Nah, just hit them with a 10mm and watch them vaporize, followed by a mushroom cloud and a bunch of dead kittens.:-)
I was told there would be no math…
I’ve always used another constant in calculating KE:
Bullet Weight (grains) x Velocity Squared (fps)/450,240
But, I have to say I like that method a lot and will put it to use!
Like that 2.22 equation. Never seen it before. Cool.
Multiply by (2.22 / 10^6) or
divide (450240) or
multiply by (.5 / 7000 / 32.163)
It’s all the same constant, just different arrangements of numbers.
Ain’t math wonderful.
Or you could just read what it is on the ammo box 😉
But what’s the formula for converting muzzle energy into hit points? 🙂
Acceleration dur to gravity at sea level 45 deg latitude is 32.1740 ft/sec squared. I’d also used the formula;
Bullet Weight (grains) x Velocity Squared (fps)/450,240 But 2*7000*32.1740=450,436 wonder where I got 450,240 from? Why did I use 32.16 for acceleration due to gravity?
Ken,
You can completely disregard the gravity component if you use either constant formula.
The 450,240 number comes from an older calculation of acceleration due to gravity. Because external ballistics measurements have been relying on the older constant (32.163 rather than 32.174) forever, most still defer to it when doing modern calculations for small arms projectiles. From a practical standpoint, the differences are close to meaningless when you consider that ME is expressed in whole numbers:
147gr @ 950fps:
2.22 rule: 294.52 ft-lbs
450,240 divisor: 294.66 ft-lbs
450,436 divisor: 294.53 ft-lbs
If I remember my sig figs properly, those are all properly expressed as 295 ft-lbs.
You’re not really disregarding gravity in the other two constants, as acceleration due to gravity is used in the calculation of the other two constants.
Btw, the 2.22 constant is using 32.1750321… as the acceleration due to gravity. Which is a pretty decent approximation.
which eggheaded cranium gigantus cares to explain how the flux capacitor works?
All this business about which value of g (acceleration due to gravity) to use shows why we really should use the metric system. Gravity has nothing to do with muzzle energy, but we have to put g in the equations because the Imperial system was thought up before the distinction between mass and weight was fully worked out.
By using SI your just moving where the gravitational constant is handled.
Consider, when you step on a scale that reads out in kilograms, and your “weight” is 84 kilograms. That 84 kilograms only equates to mass because a gravitational constant is built into the scale’s calibration.
Take the same scale to the moon and you won’t get the same reading of 84 kilograms, even though the mass is the same. Why not? Obviously, the gravitational constant for the moon is different than the earth.
SI is good for making the computations easier (mult and div by 10) but weight/mass conversions still have the same issues.
One could use the Imperial unit of mass, the slug. Just use a scale that is calibrated in slugs for the earth to get the “mass” of an object.
Why can’t I shoot as good as I can engineer?
Is this going to be on the final?
2.22 is just the approximate conversion factor from “grains foot squared per second squared” to foot pounds of energy. A foot pound of energy is the energy of one pound of force (not mass) moving through one foot of distance.
With the factor of 10^6, of course! That’s why the formula has “bullet weight (divided by 100)” and “muzzle velocity (divided by 100).”
Ummm, what?
@MichaelH:
0.5 * 9.5*10^?3 kg * (290 m/s)² ? 399.5 kg*m²/s² (=Joule)
easy as pie. since kg is a unit of mass, not weight, g plays no role whatsoever.
For the record, some years ago, a good friend of mine, Fran Paul, developed a similar,
(and possibly simpler?) bullet-energy equation that also uses the 2.22 constant.
Fran’s expression is:
Energy = 2.22 times bullet weight (grains)
times (bullet velocity/1000)*2
or using the given values in the initial post:
Energy = 2.22 * 147 * (950/1000)**2 = 294.5
Fran Paul has never climed any uniqueness for his expression as it is just a revision of the the standard physics formulation:
E = 1/2 MV**2
And as Michael H. (above) has explained, the conversion of force (lbs.) to gravity (slugs) is accomodated since the “new” constanat, 2.22 is simply 1,000,000 divided by the “old” con-stant of 450,240 which included the conversion
factors for grains to pounds, pounds to slugs, and the original 1/2 value (which becomes 2.)
And for those who’s math skills may have slipped a bit over the years, the “1,000,000” factor that both “2.22 equations” use is just the reciprocal of 1/1,000,000:
1/100 * 1/100* 1/100 = 1/1,000,000 (initial
post equation)
(1/1000)^2 = 1/ 1,000,000 (Paul equation)
Finally, “on-line” solutions are available,
as are smart-phone “apps” I suppose, but:
2.22 * bullet weight * (velocity/1000)**2
works at the range, in the woods, when the bat-teries are dead, and when the power is out. And the brain stimulation it provides may be a “good thing” too!! 🙂 🙂
—Dave Mazz